Apriori关联分析算法

工作中经常会遇到需要在一批样本中寻找若干属性来最大化覆盖这批样本的情形。这里介绍下适合这种的情景的一个关联分析算法——Apriori。

关联规则学习

维基百科：关联规则学习（英语：Association rule learning）是一种在大型数据库中发现变量之间的有趣性关系的方法。它的目的是利用一些有趣性的量度来识别数据库中的强规则。“啤酒与尿布”（这里不讨论这个案例是否真实存在）就是关联规则学习的一个典型案例。“啤酒与尿布”简单的说就是通过分析大量的消费者购物记录发现，买了啤酒的人有极大的概率会同时购买尿布。从此啤酒和尿布就这样被关联上了。

数据集及术语

这里我们使用《数据挖掘实用机器学习工具与技术》中的天气数据集。数据集描述的是天气情况以及在这种天气下是否可以出去玩。数据集如下：

outlook	temperature	humidity	windy	play
sunny	hot	high	false	no
sunny	hot	high	true	no
overcast	hot	high	false	yes
rainy	mild	high	false	yes
rainy	cool	normal	false	yes
rainy	cool	normal	true	no
overcast	cool	normal	true	yes
sunny	mild	high	false	no
sunny	cool	normal	false	yes
rainy	mild	normal	false	yes
sunny	mild	normal	true	yes
overcast	mild	high	true	yes
overcast	hot	normal	false	yes
rainy	mild	high	true	no

数据集总共有14个样本，包含12个不同的属性值，即
{'cool','false','high','hot','mild','no','normal','overcast','rainy','sunny','true','yes'}

1项集：一个属性值的集合，例如{'cool'}。
2项集：两个属性值的集合，例如{'cool','false'}。
N项集：N个属性值的集合。
覆盖量：包含N项集的样本数量。例如，{'cool','false'}的覆盖量为2。一般的覆盖量也被称为支持度。
频繁项集：达到指定覆盖量的项集。
准确率：正确预测的实例数量在关联规则所涉及的全部实例中的比例。例如，if windy=false and humidity=normal then play=yes这条规则的准确率是覆盖量({"false", "normal", "yes"})/覆盖量({"false", "normal"})= 4/4=100%。一般的准确率也被称为置信度。

Apriori算法

生成频繁项集

一般情况下，为了求得所有的频繁项集，我们需要计算所有项集的覆盖量，然后取出所有达到指定覆盖量的项集。以这里的数据集为例，我们需要计算2^12-1=4095次。
Apriori算法是一种更有效的发现频繁项集的算法，其核心原理是，如果一个项集是频繁的，那么其所有的子集也是频繁的。同样的，如果一个项集不是频繁的，那么其所有的超集也一定不是频繁的。例如，如果{"normal", "windy", "yes"}是频繁的，那么其所有的子集也是{"normal"}, {"windy"}, {"yes"}, {"normal", "windy"}, {"normal", "yes"}, {"windy", "yes"}也是频繁的，如果{"normal", "windy"}不是频繁的, 那么{"normal", "windy", "yes"}就不是频繁的。
根据上述原理，Apriori首先产生能达到指定最小覆盖量的(即频繁的)1项集，然后使用1项集产生2项集，2项集产生3项集、3项集产生4项集等。我们通过具体的例子来看。这里我们只看{"false", "normal", "yes", "high"}这个四个属性值，因为如果看全部12属性值的话会导致例子过于臃肿。

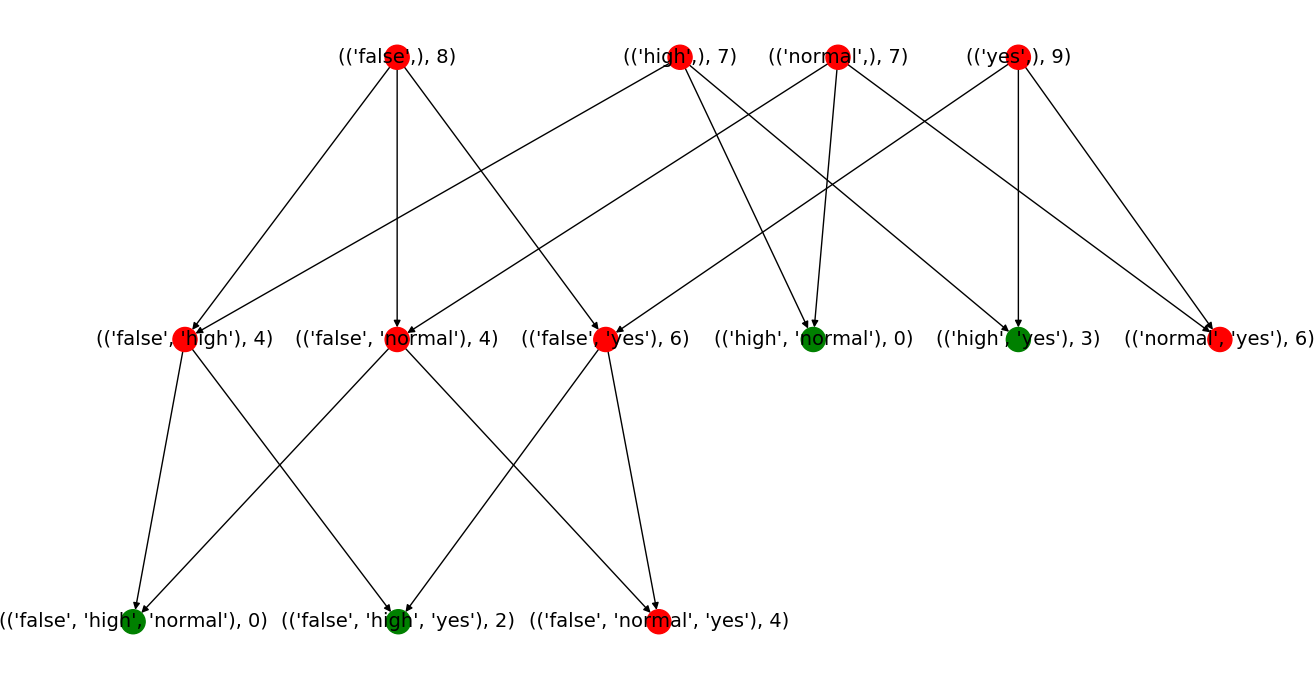
上面是{"false", "normal", "yes", "high"}在规定最小覆盖量为4的情况下从1项集到到最高3项集的计算过程。其中每个节点的名字由其代表的项集和该项集的覆盖量组成。例如第一个节点代表1项集{"flase"}，其覆盖量是8。红色的节点代表满足最小覆盖率的项集，绿色代表不满足的项集。

首先生成一项集，四个一项集都满足最小覆盖量。
根据一项集生成2项集，其中有四个2项集达到最小覆盖量，两个未达到。
根据2项集生成3项集。这里有一个技巧，一开始对1项集进行排序，然后按序生成2项集。这样我们可以得到按序排列的2项集，且每个2项集内部元素也是排序的，这里的排序都是按照字母顺序。当保证前面所述的顺序的时候，我们可以只将第一个元素相同的2项集进行合并，生成3项集。例如我们只需要将{"false", "normal"}和{"false", "yes"}组合成{"false", "normal", "yes"}，而不需要根据{"false", "yes"}和{"normal", "yes"}来生成。因为{"false", "normal", "yes"}一定可以根据{"false", "normal"}和{"false", "yes"}来生成，如果{"false", "normal"}和{"false", "yes"}不是频繁的，那么{"false", "normal", "yes"}也就一定不是频繁的。
只有一个满组最小覆盖量的3项集，无法生成下面的4项集。至此，所有的频繁项集都已经被找到。

其实到这里已经满足自己的需求了——找到若干属性（项集）来最大化的覆盖一批样本。但这只是apriori的一部分，apriori还会在产生的频繁项集中生成有效的规则。

生成有效规则

以{"false", "normal", "yes"}这个频繁项集为例。可以产生2^(3-1)-1=3个规则。对于规则{"false"} -> {"normal", "yes"}，我们称{"false"}为1前件，{"normal", "yes"}为2后件。生成规则的时候也有和生成项集差不多的技巧，即从同一个频繁项集生成规则的时候，如果一个规则不满足最小准确率，那么后件为此规则的超集的规则也不满足。例如，如果{"false", "normal"} -> {"yes"}不满足最小准确率的话，那么{"false"} -> {"yes", "normal"}和{"normal"} -> {"yes", "false"}也一定不满足。因为覆盖量({"false", "normal", "yes"})/覆盖量({"false", "normal"}) >= 覆盖量({"false", "normal", "yes"})/覆盖量({"false"})，即{"false", "normal"} -> {"yes"}的准确率一定是不小于{"false"} -> {"yes", "normal"}的准确率。有了这定论，我们就可以由1后件规则生成2后件规则，由2后件生成3后件规则，等等。

示例代码

示例代码仅供理解算法使用（没准自己在实现上还有点错误呢-.-），如果是在项目中使用，建议使用Christian Borgelt的代码。

from collections import namedtuple

def load_dataset():
    Temperature = namedtuple("Temperature", ["outlook", "temperature", "humidity", "windy", "play"])
    dataset = (
        Temperature("sunny", "hot", "high", "false", "no"),
        Temperature("sunny", "hot", "high", "true", "no"),
        Temperature("overcast", "hot", "high", "false", "yes"),
        Temperature("rainy", "mild", "high", "false", "yes"),
        Temperature("rainy", "cool", "normal", "false", "yes"),
        Temperature("rainy", "cool", "normal", "true", "no"),
        Temperature("overcast", "cool", "normal", "true", "yes"),
        Temperature("sunny", "mild", "high", "false", "no"),
        Temperature("sunny", "cool", "normal", "false", "yes"),
        Temperature("rainy", "mild", "normal", "false", "yes"),
        Temperature("sunny", "mild", "normal", "true", "yes"),
        Temperature("overcast", "mild", "high", "true", "yes"),
        Temperature("overcast", "hot", "normal", "false", "yes"),
        Temperature("rainy", "mild", "high", "true", "no")
    )
    return dataset

def count_support(dataset, itemset):
    """compute the support for given item set
    Args:
        dataset (iterable): the whole dataset, for example: ((1,2), (1,3))
        itemset (iterable): item set, for example: (1, 3)

    Returns:
        support (int): the number of samples containing the given item set
    """
    support = 0
    for sample in dataset:
        for item in itemset:
            if not item in sample:
                break
        else:
            support += 1
    return support

def generate_combination(candidates):
    """generate combinations. This is used both in frequent sets and rules.
    """
    #check the order, can be removed
    for i in range(len(candidates)-1):
        assert candidates[i] <= candidates[i+1]
    for i in candidates:
        for j in range(len(i)-1):
            assert i[j] <= i[j+1]

    number = len(candidates)
    for i in range(number-1):
        for j in range(i+1, number):
            item1 = candidates[i][:-1]
            item2 = candidates[j][:-1]
            if item1 == item2:
                new = list(item1)
                new += [candidates[i][-1], candidates[j][-1]]
                yield new
            else:
                break

def generate_frequentsets(dataset, support=4):
    """
    Args:
        dataset (iterable): the whole data set
        support (int): support
    """
    data_len = len(dataset)
    candidates = {}
    efis = []
    fis = set()
    for sample in dataset:
        fis.update(set(sample))
    for k in sorted(list(fis)):
        esup = count_support(dataset, ((k, )))
        if esup >= support:
            efis.append([k,])
            candidates[(k,)] = esup
    while 1:
        new_efis = []
        for efi in generate_combination(efis):
            esup = count_support(dataset, efi)
            if esup >= support:
                candidates[tuple(efi)] = esup
                new_efis.append(efi)
        efis = new_efis
        if len(efis) == 0:
            break
    return candidates

def generate_rules(frequentsets, min_accuracy):
    """used to generate rules
    Args:
        frequentsets (dict): the whole frequent sets
        min_accuracy (int): the minimum accuracy
    """
    rules = []
    for fset in frequentsets:
        if len(fset) > 1:
            candidates = []
            for rule in fset:
                left = tuple(sorted(list(set(fset)-set((rule,)))))
                #print(left, rule, float(frequentsets[fset])/frequentsets[left])
                if float(frequentsets[fset])/frequentsets[left] >= min_accuracy:
                    candidates.append((rule,))
                    rules.append((left, (rule,)))
            while 1:
                new = []
                for rule in generate_combination(candidates):
                    left = tuple(sorted(list(set(fset)-set(rule))))
                    if not left:
                        break
                    print(left, rule, float(frequentsets[fset])/frequentsets[left])
                    if float(frequentsets[fset])/frequentsets[left] >= min_accuracy:
                        rules.append((left, rule))
                        new.append(rule)
                if not new:
                    break
                candidates = new
    return rules

if __name__ == "__main__":
    fs = generate_frequentsets(load_dataset(), 3)
    rules = generate_rules(fs, 1)
    print(rules)

算法缺点

Apriori是一种自下而上的项集建立算法，即先算小的项集，然后从小的项集逐步生成更大的项集。每轮计算中都会要保存用于生成更大项集的所有小的项集。在最坏的情况下，这个每轮计算中需要的小项集是指数增长的。并且每次计算项集的覆盖量都需要重新扫描整个数据集。所以Apriori一般会很慢且消耗大量内存。举个实际使用的例子，在包含60多个不同属性值的20多个相似度较高的样本中计算频繁项集，内存在一段时间后达到了20G（python实现的算法），然后自己就手动kill了。针对Apriori算法的缺点，有很多衍生的算法，有兴趣的话可以看看。

参考文档

《数据挖掘实用机器学习工具与技术》
Machine Learning in Action
wiki