前面讲了Apriori关联分析算法,提到Apriori就不能不提FP-Growth。今天我们就来看下FP-Growth的原理。
数据集
这里仍使用Apriori中用到的数据集(《数据挖掘 实用机器学习工具与技术》中的天气数据集)。其它概念的性的定义也可以参考Apriori里面的介绍。
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| sunny | hot | high | false | no |
| sunny | hot | high | true | no |
| overcast | hot | high | false | yes |
| rainy | mild | high | false | yes |
| rainy | cool | normal | false | yes |
| rainy | cool | normal | true | no |
| overcast | cool | normal | true | yes |
| sunny | mild | high | false | no |
| sunny | cool | normal | false | yes |
| rainy | mild | normal | false | yes |
| sunny | mild | normal | true | yes |
| overcast | mild | high | true | yes |
| overcast | hot | normal | false | yes |
| rainy | mild | high | true | no |
FP-growth算法
生成频繁项集
FP-growth算法首先计算属性值的频数,并过滤掉不符合覆盖量属性值,然后按频数从大到小进行排序。这里我们指定最小覆盖量为6。下表为计算后的结果:
| 属性值 | 频数 |
|---|---|
| yes | 9 |
| false | 8 |
| high | 7 |
| normal | 7 |
| true | 6 |
| mild | 6 |
| 5 | |
| 5 | |
| 5 | |
| 4 | |
| 4 | |
| 4 |
对数据集第一次扫描完成后,需要对其进行第二次扫描,并在这个过程中建立树结构。树节点的插入顺序按照频数顺序插入,频数高的属性值优先插入树中,这可以让多个实例共享频繁出现的项。我们还是使用具体的例子来解释这个过程。
指定最小覆盖量为6后,我们给满足条件的样本建立FP树。对第一个样本,
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| sunny | hot | high | false | no |
第一个样本中false和high满足指定最小的覆盖量,且根据我们上面的统计false出现的频数要大于high。所以我们首先将false插入到root节点后面,然后再将high插入到false后面。结果如下图所示。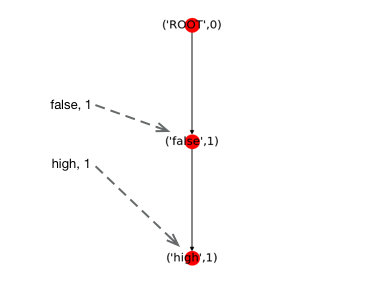
树中每个节点记录着节点对应的属性值,以及从root节点开始(不包含root节点)沿箭头方向遍历到此节点组成的N项集的频数。例如,(‘false’,1)代表着(‘false’)这个一项集出现了1次。(‘high’,1)代表着(‘false’, ‘high’)这个二项集出现了1次。FP树的左边是头部链表(虚线箭头组成的链表),其将具有相同属性值的节点链接起来。
接着,我们将第二个样本插入到树中。
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| sunny | hot | high | true | no |
同样的,我们先对第二个样本中满足指定覆盖量的属性值按频数排序,即high, true。并按照顺序将其插入树中。
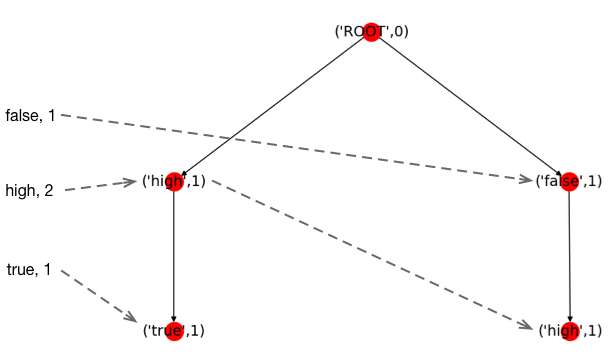
接着是第三个样本,
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| overcast | hot | high | false | yes |
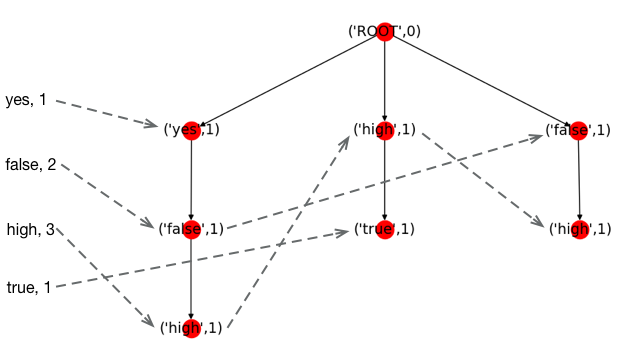
第四个样本,
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| rainy | mild | high | false | yes |
这里满足指定覆盖量的属性值按频数排序后是yes, false, high, mild。同样,我们先插入yes节点。因为已经存在从root指向yes的路径,所以,我们直接复用,只需要将yes节点的计数加1就好。插入第二节点也是一样,因为路径存在,只需要将false的计数加1。后续节点依次按照规则加入到树中。这就是为什么要按属性值频数排序,然后依次插入的原因,这样可以尽可能减少路径的重复,从而达到对树的压缩。
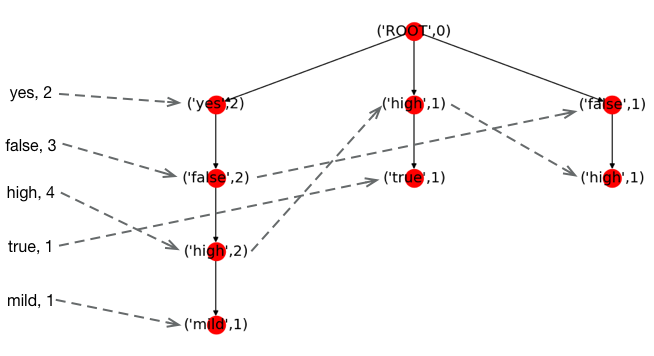
最终我们建立的FP树如下图所示。
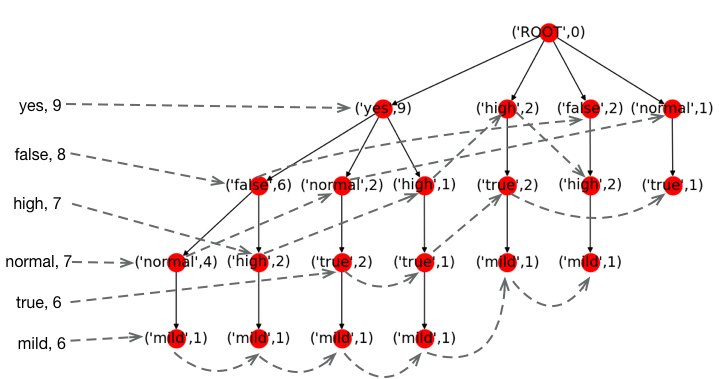
当FP树建立完成后,我们就可以进行频繁项集的挖掘。我们按照头部链表从底部向上依次遍历(实际上可以按照任意顺序对头部链表进行遍历)。首先,我们将mild加入频繁项集中,即{‘mild’}。我们建立一个由包含mild的样本建立的FP树,如下图所示。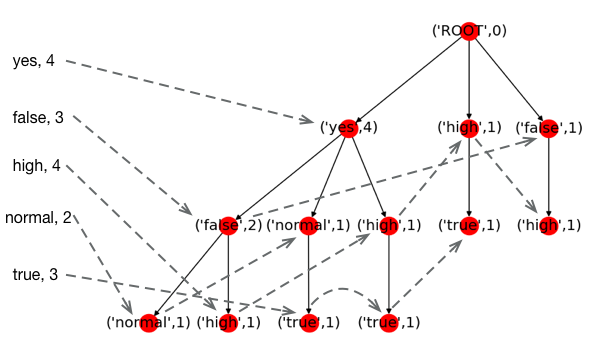
该FP树建立过程,不需要重新扫描数据集,而是根据上面包含mild的完整的FP树生成。首先我们根据头部链表找到所有包含mild的节点,然后只保留包含mild的分支。同时从mild节点向上传播计数,即每个节点的计数是它所有子节点的计数和。
遍历该FP树的头部链表,属性值的最大频数为4,不能达到我们指定的最小覆盖量6。所以{‘mild’}不可能再增大,即频繁项集不可能包含mild。如果新建立的FP树仍有若干属性值满足最小的频数要求,这里假设yes和false满足要求,那么我们需要将yes和false依次加入到备选项集中,然后建立相应的FP树,这便形成了递归。
生成有效规则
有效规则的生成和Apriori相同。
代码
可以参考Machine Learning in Action。这里的实现跟本文提到的略有不同,主要体现在生成新的FP树上。
实际使用中可以用Christian Borgelt实现的算法。
参考文档
- 《数据挖掘 实用机器学习工具与技术》
- Machine Learning in Action
- wiki